[CG] Depth, Z and W, and Clip Space
Convention
아래와 같은 컨벤션을 바탕으로 작성한다.
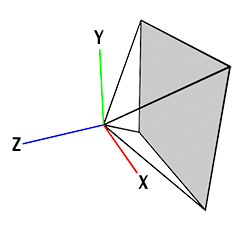
- 오른손 좌표계 (right-handed system)
- 카메라는 -Z방향을 바라본다
- row-vector convention
- row-major (memory layout)
- near plane을 image plane으로 삼는다
- NDC: [0, 1]
Homogeneous coordinates
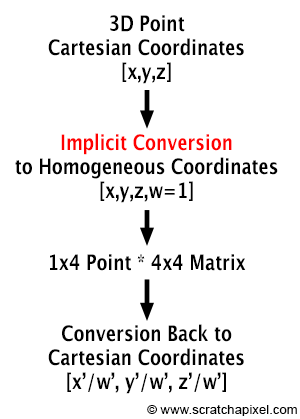
좌표계간 변환
cartesian 좌표계와 homogeneous 좌표계간 변환은 w=1인 상태로 하여금 가능하다.
- cartesian -> homogeneous: 기존 (x,y,z) 3차원 카테시안 좌표에 w=1 추가
- homogeneous -> cartesian: 스칼라 배를 통해 w=1로 만든 후 w좌표를 제외한 나머지 (x', y', z')만 취한다
homogeneous (동등, 동차)라는 것의 의미
어떠한 좌표의 스칼라 배에 대해 동등한 (카테시안) 좌표로 취급한다는 뜻이다. 예를 들어, (4,6,8,2)라는 좌표는 (2,3,4,1)이라는 좌표와 동등한 카테시안 좌표 (2,3,4)이다.
w좌표 도입의 효과
w좌표의 도입으로 인해 기존 3차원 카테시안 좌표계에서는 비선형(non-linear) 변환이었던 것이 선형(linear) 변환이 된다. 즉 4x4 행렬이 되면서 기존의 비선형 변환을 행렬 곱으로 표현할 수 있다.
- translate 변환
- projection 변환 (perspective divide 미포함)
point(점) & vector(방향)
- point: w!=0
- vector: w=0
w=0이기 때문에, vector(방향)은 translation(평행 이동)의 영향을 받지 않는다. 수학적으로 w=0인 homogeneous 좌표는 무한히 멀리 있는 점(point of infinity)를 의미하기도 한다. 수치적으로도, 0으로 나눴을 때 무한이 되는 것으로 알 수 있다.
Z 좌표 그리고 W 좌표
view space까지는 모든 점들의 w값에 변동이 없다. 즉 w=1이다. (3차원 카테시안 좌표계나 다름 없다) 그러다가 투영 행렬을 곱해 projection 변환을 거치고 나면 w값은 직전 view space에서의 깊이(depth) 값이 된다.
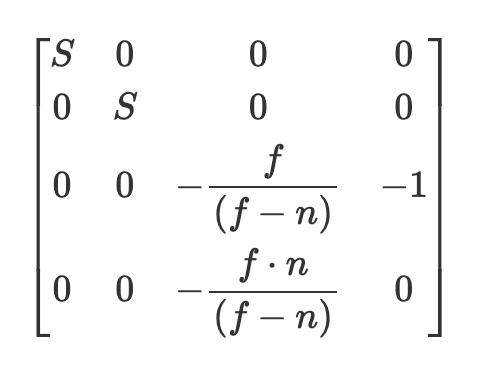
view frustum이 대칭일 때의 projection matrix (비대칭일 때보다 간단한 형태)
네 번째 열이 바로 w값을 결정짓는 부분인데 w = z * (-1)인 것을 볼 수 있다. (z가 아닌 -z인 이유는 카메라가 -z 방향을 가리키고 있기 때문에 카메라 기준에서의 깊이를 구하려면 부호를 뒤집어주어야해서 그렇다. 쉽게 'distance = 절댓값' 같은 것이라고 생각하자)
즉, clip space에서 w는 '카메라로부터의 깊이 값' 그 자체를 의미한다.
그럼 투영 행렬을 적용한 후 z는 뭘 의미하게 될까?
z=n, w=1 그리고 z=f, w=1을 위 행렬의 세 번째 열에 대입해 clip space의 z좌표를 구해보면,
- z=n일 때 0
- z=f일 때 f
가 된다. 즉 [0, f]로 매핑된다.
사실 clip space에서의 좌표 값은 ndc space로 가는 중간 과정으로, 이후 w로 나눠야하기 때문에 최종적으로 z의 값은 다음과 같다:
$$ z_{ndc} = \frac{z_c}{w_c} = \frac{-\tfrac{f}{f-n}z_v - \tfrac{fn}{f-n}}{-z_v} = \frac{f}{f-n} + \frac{fn}{(f-n)z_v} $$
즉, 최종적으로 z값은 [0, 1]로 매핑된다.
아래의 이미지가 z, w, 그리고 z/w값에 대해 아주 잘 설명해주고 있다.
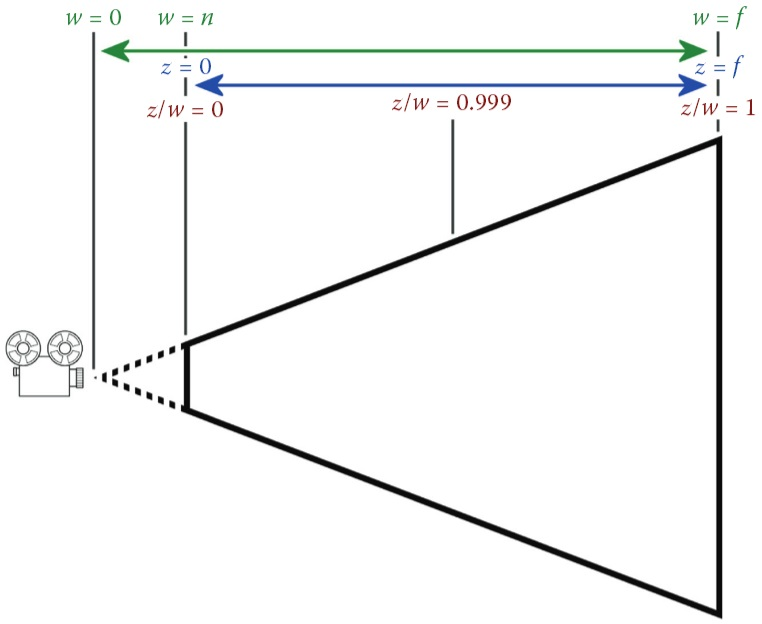
투영 행렬 적용 후 z, w, z/w값
- z: [0, f], near plane으로부터의 (상대적) 깊이
- w: [0, f], 카메라로부터의 깊이
- z/w: [0, 1], near부터 far까지를 전체 구간으로 봤을 때 (비선형적) 깊이 (f에 가깝지 않은 지점이 z/w=0.999인 점도 주목할 만한데 z/w라는 값이 '비선형적'임을 나타낸다.)
결국 z와 w가 이렇게 각기 존재하는 이유는 3D 공간을 2D로 렌더하는데 있어서 viewing frustum 상에서의 깊이도 고려해야하고, 카메라로부터의 깊이도 고려해야하기 때문이다.
Clip Space가 존재하는 이유
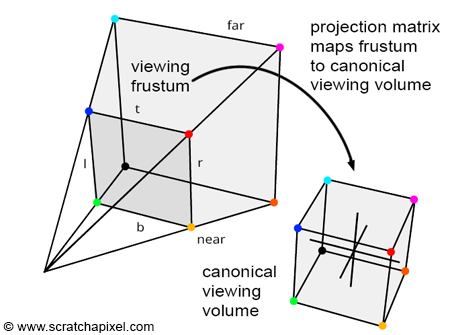
viewing frustum에서 canonical viewing volume으로 이행하는 과정:
'투영행렬 적용' 그리고 'perspective divide'
![view space -> clip space -> NDC (이미지에서는 [-1,1])](/posts/2025/08/why-clip-space-exist/Pasted%20image%2020250825023711.png)
view space -> clip space -> NDC (이미지에서는 [-1,1])
clip space에서 NDC로 이행하는 과정은 간단하다. perspective divide를 하면 된다.
이때 중요한 점은 perspective divide가 비선형(non-linear) 변환이라는 것이다.
이 변환을 거치고나면 좌표간 간격 비율이 달라진다. (각 좌표마다 w값이 다르므로, 모든 좌표에 대해 같은 값으로 나눗셈을 하는게 아니다. 따라서 전체 공간의 확대/축소가 이루어지는 스케일링과는 다르다.)
이 부분에서 왜 clipping 작업을 굳이 'clip space'라는 단계를 두어 수행하는지 알 수 있다. 비선형 변환인 perspective divide를 수행하고 나면 공간이 비선형적으로 찌그러지기 때문이다. 그러면 선형 공간에서는 단순히 직선-평면 관계로만 판단하면 됐던 것들이 곡선이 되면서 판단하기 복잡해진다.
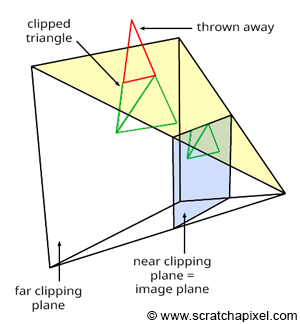
clipping 작업: viewing frustum을 기준으로 필요없는 것을 날려버린다
게다가 clipping 단계에서도 정점간 interpolate를 수행하여 fragment의 속성 값을 구해야하기 때문에, 선형 공간이 아니라면 곤란하다. (정점간 interpolate는 본래의 선형 공간을 기준으로 수행되어야 할 것이다.)
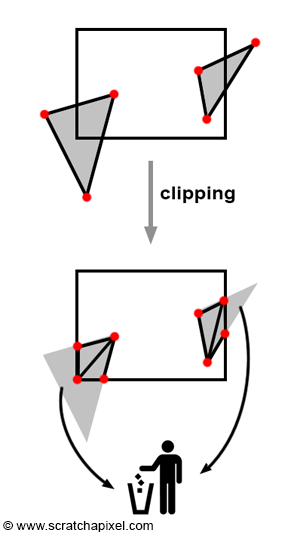
clipping 수행 과정에서 interpolate가 필요:
삼각형의 일부만 남기는 경우도 있다
추가로, w=0 근처의 점들의 경우 perspective divide를 수행하면 값이 폭발적으로 커지기 때문에 그런 특이점을 회피하려는 목적도 있다.
[!abstract] Clip space는 단순한 중간 단계가 아니라, 비선형적인 perspective divide 전에 clipping과 interpolation을 처리하기 위한 필수 공간이다. z와 w를 분리해 깊이를 표현하고, 파이프라인을 안정적이고 단순하게 만든다.